No âmbito do projeto especial em colaboração com a Corretora Prime EXANTE, o Insider.pro dá início à série de artigos de divulgação científica "Matemática do Infinito e a Realidade das Finanças" do doutor em Física e Matemática Viktor Argonov sobre a teoria das probabilidades e meios inesperados da sua aplicação às finanças. Ao longo de centenas de anos, os matemáticos têm operado sem sombra de dúvida com várias magnitudes infinitas: multiplicam, dividem, comparam várias infinidades entre si etc. As magnitudes infinitas são uma das categorias mais abstratas de matemática, mas às vezes elas afetam a nossa vida real. Em particular, a vida financeira.
A teoria das probabilidades tem paradoxos quando as fórmulas prometem aos traders ganhos eternos e à empresa uma prosperidade sem fim. Estas situações podem parecer engraçadas e os matemáticos uns "cientistas loucos". Mas nem tudo é tão simples. Acontece às vezes que as infinidades, quando penetram na vida, podem afetá-la bastante. Vamos abordar alguns destes paradoxos nesta série.
Na teoria das probabilidades a teoria do passeio aleatório tem grande importância. A formulação inicial é bem abstrata: um ponto move-se em várias direções de uma maneira aleatória. Mas na vida real este problema pode ser aplicado concretamente, incluindo às finanças. Porém, para começar, vamos conhecê-lo com um exemplo de humor e não de economia: sobre um homem bêbado que se move aleatoriamente.
Os bêbados itinerantes na teoria
Imaginemos um bêbado que saiu de um bar e quer ir para algum lugar. Mas ele está tão desorientado que dá cada passo numa direção aleatória. Ele não se lembra em que direção acabou de ir. Porém, o bar é situado num impasse de uma ruela estreita com cercas. O movimento pode ser apenas em duas direções: a partir do bar e de volta para lá. O bêbado dá sempre o primeiro passo para frente (do bar), depois disso o seu movimento é aleatório, mas só em duas direções possíveis: um passo em frente, um passo atrás, um passo em frente, um passo em frente, um passo atrás, um passo em frente, um passo em frente etc. A matemática chama a este processo passeio aleatório unidimensional.
Adicionemos outra condição: se durante o passeio, o bêbado voltar por acaso ao bar, os guardas vão levá-lo ao bar e irão pô-lo a dormir no sofá.
Imaginemos que há muitos bêbados no bar. De vez em quando eles saem do bar, mas podem apenas passear pela rua estreita. E nós estamos a observar isto, desenhamos a trajetória de cada um e marcamos a hora em que a pessoa volta ao bar.
Faremos três perguntas:
- A que distância do bar, em média, estará um bêbado depois de N passos?
- Qual será o tempo mediano em que os bêbados voltarão ao bar (ou seja, o tempo que vai demorar para metade dos bêbados voltarem)?
- Qual será o tempo médio da volta dos bêbados (o tempo total de passeio de todos os bêbados dividido pelo seu número)?
A primeira pergunta tem uma resposta simples, conhecida pelos estudantes como: a raiz de N. Se um bêbado fizer cem passos, provavelmente estará a 10 passos de distância do bar. Se fizer 10 mil passos, então estará a 100 passos de distância.
A segunda pergunta pode ser respondida com especulações mais simples. Segundo o problema, o primeiro passo do bêbado será em frente. Depois, ele dará um passo atrás com a probabilidade de 1/2. Então, depois de dois passos a metade dos bêbedas voltarão para o bar, por isso o tempo mediano de volta é igual a dois passos.
Mas a terceira pergunta tem uma resposta estranha, sobre a qual não falam normalmente nas universidades e que é particularmente surpreendente de ouvir depois das respostas às primeiras duas perguntas. Muitas pessoas confundem o tempo mediano e médio (como por exemplo, salário mediano e médio). Mas estas magnitudes podem diferenciar bastante. no nosso caso, como provaram os matemáticos, o tempo médio de volta do bêbado ao bar é igual... à infinidade. Pelo menos, é o que indicam as fórmulas matemáticas.
Como é possível? Vamos tentar entender.
Os bêbados itinerantes num exercício intelectual
Lembremos mais uma vez o que é uma magnitude média e como é contada. Para achar a locação média de um bêbado depois de N passos e o tempo médio da sua volta, é preciso fazer o exercício muitas vezes, em cada caso medir estas magnitudes, e depois achar a média aritmética.
Vamos supor que no início vemos cinco pessoas e recebemos resultados simples. Duas pessoas voltaram depois de dois passos (em frente e para trás), outro voltou depois de 4 passos (em frente - em frente- para trás - para trás) e outros dois deram 8 passos cada um por uma trajetoria complicada. O tempo mediano de volta é de três passos, o que é perto da avaliação teórica (2 passos). O tempo médio de volta é igual a (2*2+1*4+2*8)/5=24/5=4.8 passos. Parece que o tempo é curto e que não há nenhuma "infinidade".
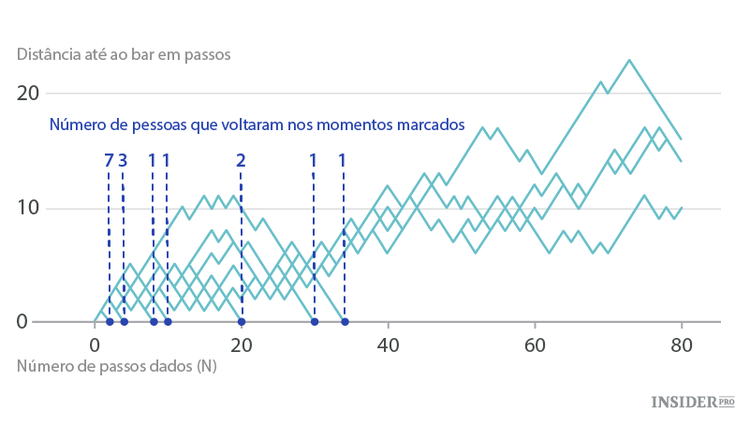
Mas cinco pessoas é muito pouco para uma estatística boa. Seguidamente decidimos monitorar vinte pessoas. E recebemos o resultado mostrado no gráfico abaixo.
A metade dos participantes da "corrida" (10 pessoas), assim como antes, voltaram depois de 2 ou 4 passos. Outras 6 pessoas voltaram depois de 10 ou 30 passos. Mas as restantes 4 pessoas foram "em direção desconhecida", e os seus passeios nem couberam no gráfico. Eles voltaram depois de 140, 198, 202 e 298 passos, respetivamente.
O desvio médio dos bêbados a partir da sua localização inicial corresponde bem à teoria. Por exemplo, depois de 20 passos a teoria prevê a distância de 4 ou 5 passos (a raiz de 20). O gráfico no momento N=20 há trajetorias de apenas 7 pessoas (as outras já voltaram para o bar e estão a dormir e por isso excluímo-los da consideração). Duas delas acabaram de voltar ao bar (o seu desvio é igual a zero), uma pessoa está a dois passos do bar, outra a quatro, duas pessoas - a seis passos e a última - a 10 passos. O desvio médio do bar é igual a (2*0+1*2+1*4+2*6+1*10)/7=28/7=4 passos. Igual à teoria.
O tempo mediano de volta tornou-se duas vezes maior que a avaliação teórica — 4 passos. Mas este erro é aceitável, com o nosso número de exercícios pequenos.
É muito mais difícil contar o tempo médio de volta. Ele é igual a (7*2+3*4+1*8+1*10+2*20+1*30+1*34+1*140+1*198+1*202+1*298)/20 = 986/20 = 49,3 passos. Este resultado não tem nada a ver com o anterior, devido a quatro "aventureiros". Por que não os considerámos antes? Coincidência? Será que é melhor observar ainda mais bêbados, e então poderemos achar o número real do tempo médio do passeio?
O truque do problema é que quanto mais abrangentes são as experiências que fazemos, maior será o tempo médio de volta. A metade de bêbados vai sempre voltar depois de 2 a 4 passos. Mas entre o resto vai sobrar uma parte de "aventureiros" que podem ir para muito longe do bar.
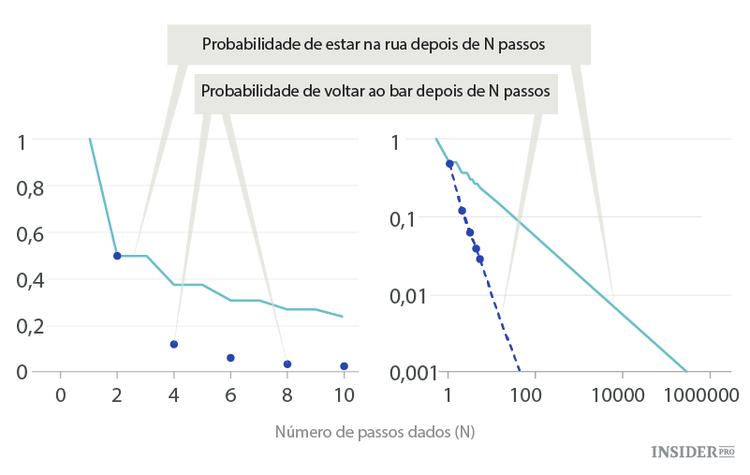
Os gráficos da probabilidade de os bêbados estarem na rua depois de N passos e a probabilidade da sua volta ao bar exatamente no passo N (em escala linear e logarítmica em ambos os eixos). Ambos os gráficos com o N grande são funções de potência, por isso em escala logarítmica dupla aparecem como retas
Os matemáticos derivaram uma fórmula, segundo a qual é possível contar a probabilidade de volta de um bêbado ao bar no passo número N e a probabilidade de ele estar na rua depois do passo N. Em termos gerais, estas fórmulas são complicadas, e nós apenas citamos os gráficos. O bêbado pode voltar ao bar apenas ao fazer um passo ímpar. No segundo passo a probabilidade do bêbado voltar ao bar e a probabilidade de ele ficar na rua é igual a 1/2. A probabilidade de voltar ao bar no quarto passo é igual a ⅛, e a probabilidade de ficar na rua é igual a ½-⅛=⅜. Se o N for grande, a probabilidade de voltar ao bar é proporcional a N na potência 3/2, e a probabilidade de estar ainda na rua é igual à raiz de N.
Isto significa que uma parte dos bêbados vai passear durante muito tempo. Por exemplo, se N=100, um em cada dez participantes da "maratona" estará na rua, se N=1000 — um em cada trinta, se o N=10.000 — um em cada cem. Na matemática a estas voltas longas com estatísticas crescentes chamamos "voos de Lévy". A característica paradoxal dos voos de Lévy é que à medida que aumenta o número de exercícios intelectuais, o seu tempo médio cresce.
Se houver 10 pessoas, então o bêbado mais "aventureiro" andará cerca de 100 passos, e a maioria do resto de 2 a 4 passos.
O comprimento do seu passeio pode facilmente exceder o dos passeios dos outros participantes. A contribuição deles é de 20 a 40 passos, e a dele será de 100 passos. O tempo médio de volta é de 12 a 14 passos.
Se considerarmos 100 pessoas, então o bêbado mais "aventureiro" dará 10 mil passos, e a maioria dos outros — de 2 a 4 passos. Desta vez a sua contribuição pode ser ignorada. O tempo médio de volta será de cerca de 100 passos.
O comprimento do caminho do participante mais "aventureiro" normalmente será proporcional ao número quadrado dos participantes, e o tempo médio de volta será igual ao número dos participantes, À medida que cresce o número de participantes, o tempo médio vai aproximar-se da infinidade, embora as próprias trajetórias tenham um final. É aí que está um resultado estranho, embora exato do ponto de vista de matemática e possível de provar (com exceção do limite do número real possível de testes).
Este resultado tem importância crucial não só na pergunta sobre o movimento dos bêbados, mas também numa questão mais relevante para nós — sobre o movimento dos capitais.
O movimento das cotações das ações e taxas de câmbio, enriquecimento e falência dos participantes de jogos de azar e empresas reais de produção — tudo isto pode ser modelado com processos aleatórios que muitas vezes se limitam ao passeio aleatório de um ponto por uma linha reta. E neste caso também existem "voos de Lévy". Falaremos nisto nos próximos artigos.